Hola chicos, esta vez daremos información sobre ''Logaritmo''. Una pieza muy importante en matemáticas ya sea en el bachillerato tanto como en la Universidad.
Logaritmo.
En matemáticas,
el logaritmo de un número —en una base de logaritmo
determinada— es el exponente al cual hay que elevar la base para
obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque
1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera
que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.
Para representar la
operación de logaritmo en una determinada base se escribe la abreviatura log y
como subíndice la base y después el número resultante del que deseamos hallar
el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando
se sobreentiende la base, se puede omitir.
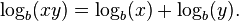
Propiedades de los logaritmos
No existe el logaritmo de un número con base negativa.
No existe el logaritmo de un número negativo.
No existe el logaritmo de cero.
El logaritmo de 1 es cero.
El logaritmo de a en base a es uno.
El logaritmo en base a de una potencia en base a es igual al exponente.
El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
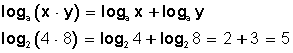
El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:
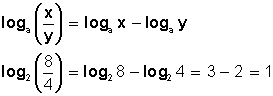
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:
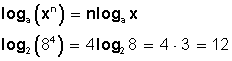
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
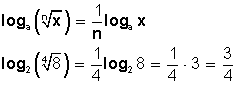
Cambio de base:
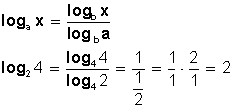
Logaritmos decimales:
Son los que tienen base 10. Se representan por log (x) (ya vimos que la base 10 no se escribe, queda implícita).
Logaritmos neperianos o naturales:
Son los que tienen base e. Se representan por ln (x) o L(x) (ya vimos que la base e tampoco se escribe, se subentiende cuando aparece ln).
Algunos ejemplos de logaritmos neperianos son:
ln 1 = 0; puesto que e0 = 1
ln e2 = 2; puesto que e2 = e2
ln e−1 = −1; puesto que e−1 = e−1
El número e tiene gran importancia en las Matemáticas. No es racional (no es cociente de dos números enteros) y su valor, con seis cifras decimales, es
e = 2,718281...
No hay comentarios:
Publicar un comentario